Emacs Calc for Programmers and Computer Scientists

Introduction

As a research student in information engineering and a programmer, I often need to calculate memory addresses, convert data transmission rates or convert binary in hexadecimal and vice versa. Guess what, a computer can all do that. I'm a Emacs nerd but for those calculations I was using duckduckgo and wolfram alpha. They do a good job, however, this approach is quite cumbersome, especially wolfram alpha is pretty slow sometimes. Thus, I took a closer look at Emacs Calc to find out how to achieve the same thing within Emacs.

Why Emacs?

I don't understand the question. But seriously: When I do programming I'm already within Emacs; when I do research, I use org-mode to protocol my progress and my thinking. Therefore, it makes sense for me to use Emacs for this task too. Beside that, there are other advantages to use Emacs Calc:

1. Like Emacs itself, Calc is open-source and extensible. You do not need to wait until the next version gets released. If you are curious enough you can fully understand how Calc is developed. Additionally, like any other Emacs mode, Calc provides various ways to extend it. We will see in Section Units how we can add more units to Calc.
2. Calc can be used for more complex calculation. Calc is able to handle vectors and matrix manipulations, rational numbers, complex numbers and so on. Karthik called it the poor man's mathematica.
3. You can be pretty efficient if you have mastered the keybindings and got you head around the RPN (Reverse Polish Notation). Researchers show that RPN is superior compared to the algebraic notation in terms of calculation speed and accuracy.

Numeral System

This is one of the first facts that I learned in university that blow my mind: A number is an abstract construct and can be divided in its value and its representation. The value for the number five is always the same, no matter how you represent it: 5, V, five, or 101. This means the number five exists even if we would have not a system to represent it. As a programmer and computer scientist, however, you have to juggle with numbers in different representations like binary, hexadecimal and octal. Lets take a look how we can do that with Calc.

Enter Numbers with different Base

If you enter numbers in Calc, it will displays these in the current radix notation, which we will cover in the next section. By default the radix mode is set to decimal notation (base 10). If you would like to enter a numbers with different base you have to press # and enter the number in the following form: <number_of_base>#number. Some examples:

Description	Emacs Calc	Base 10
Binary	2#11110101	245
Octal	8#27	23
Hexadecimal	16#FFFF	65535

Easy Peasy! There are, however, two interpretations of binary numbers namely signed and unsigned integers. Let' image we have a word size of w = 8 bits, then unsigned integer can represent numbers from 0 to –2^w-1 and signed integer numbers from -2^(w-1) to 2^(w-1)-1. The last one is called two's complement. By default, Calc has a word size of 32 bits, which can be changed with b w (calc-word-size). You can enter twos-complement number with double number signs, like the following: 2##11110101. This number is interpreted as -11 with a word size of 8 bits, instead of 245. As mentioned before, all numbers are automatically converted to the current radix mode.

Change Radix Mode

This means there is a difference between how you enter the numbers and how the numbers are displayed. To change the display, you have to change the radix mode. To change the current radix mode, you have to press d r (calc-radix) and enter an integer from 2–36. There are, however, shortcuts for the most convenient ones:

Shortcut	Representation
d 2	Binary
O d 2	Two-complement Binary
d 6	Hexadecimal
d 8	Octal
d 0	Decimal

This makes it super easy to enter any number, no matter in which representation it is and change it to whatever you like. To better compare a number represented in binary, you can enable leading zeros with d z (calc-leading-zeros). This is all for the display, let's talk about what you can do with these binary numbers.

Binary Number Operation

To switch from signed to unsigned integers, Calc provides a function called b c (calc-clip). This function clips the current number by reducing it by 2^w. With a word size of 8 bits, you can change a number from signed to unsigned with b c; with a word size of -8, you change a number from unsigned to signed. Example:

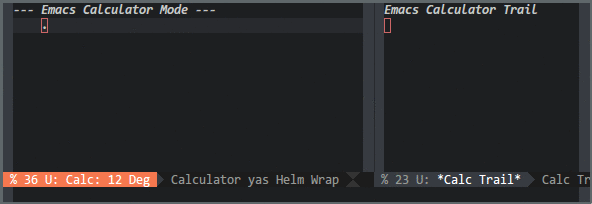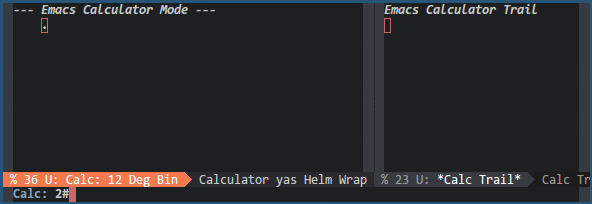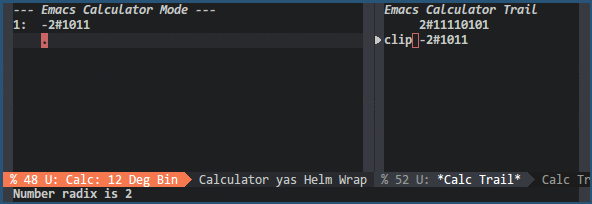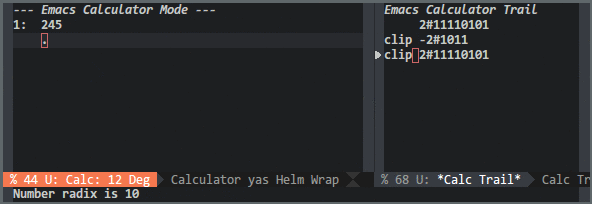
The sign of the word size also influences the result of the following binary operations:

Keybinding	Calc Function	Description
b a	(calc-and)	Bitwise AND
b o	(calc-or)	Bitwise OR
b x	(calc-xor)	Bitwise XOR
b n	(calc-not)	Bitwise NOT
b d	(calc-diff)	Bitwise difference
b r	(calc-rshift-binary)	Bitwise right shift by 1 bit
b l	(calc-lshift-binary)	Bitwise left shift by 1 bit

Did you ever ask yourself how many 1s are set on binary representation of the number 424242? No? I will show you nevertheless how you can do this in Calc. If 424242 is on the stack, we first unpack the number with b u into sets. Then we count the number of set bits with v #. The result is 10.

Units

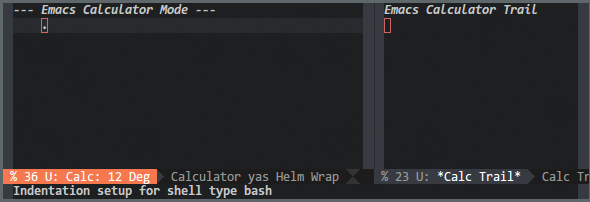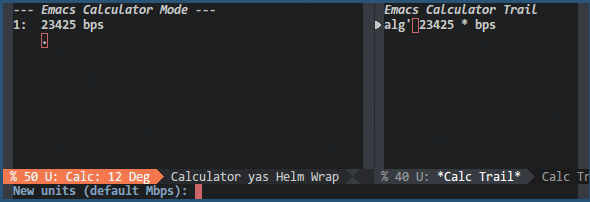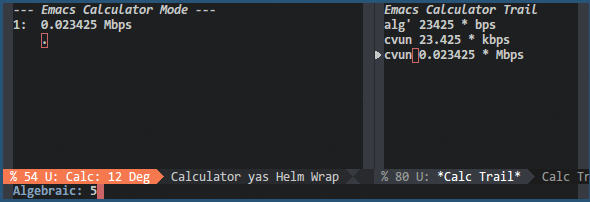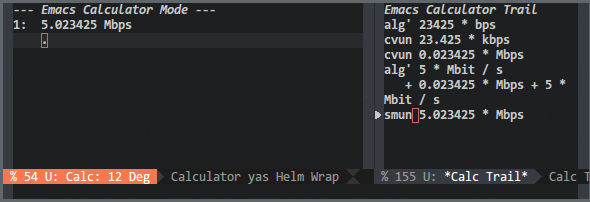
Calc understands units and has a couple of predefined units already included. You can take a look at the predefined units by pressing u v (calc-enter-units-table). To push a number with a unit to the stack you can press ' (calc-algebraic-entry) and just type 23 m. If you would like to convert that unit to cm for example, just type u c (calc-convert-units) and type cm. You can even calculate with these units. You can try to add 23 m and 42 cm together. Calc will display 23 m + 42 cm. If you press u s (calc-simplify-units) you will get 23.42 m.

There is, however, one disadvantage with the predefined units. If you look closely at the predefined units, there are no digital information units. Don't worry, we are in Emacs, we can change anything we like. Calc provides a variable called math-additional-units where additional units can be added. This variable must be formatted like math-standard-units. The following Emacs Lisp snippet will add digital information units to Calc:

(setq math-additional-units
      '((bit    nil           "Bit")
        (byte   "8 * bit"     "Byte")
        (bps    "bit / s"     "Bit per second"))
        math-units-table nil)

The snippet will also set math-units-table to nil to rebuild the combined units table. The snippet does not need to define unit prefixes like (K)ilo, (M)ega or (G)iga, since Calc is already aware of these SI prefixes. In the following gif you can see its usage:

Conclusion

Emacs Calc is a powerful tool that is only a keybinding C-x * c away. I only highlighted the features that are particular interesting for programmers and computer scientists. It is worth looking at the fine manual.